2025
Real-time applicability of emulated virtual circuits for tokamak plasma shape control
P. Cavestany, A. Ross, A. Agnello, A. Garrod, N. Amorisco, G. K. Holt, K. Pentland, J. Buchanan
2025 IEEE Conference on Control Technology and Applications
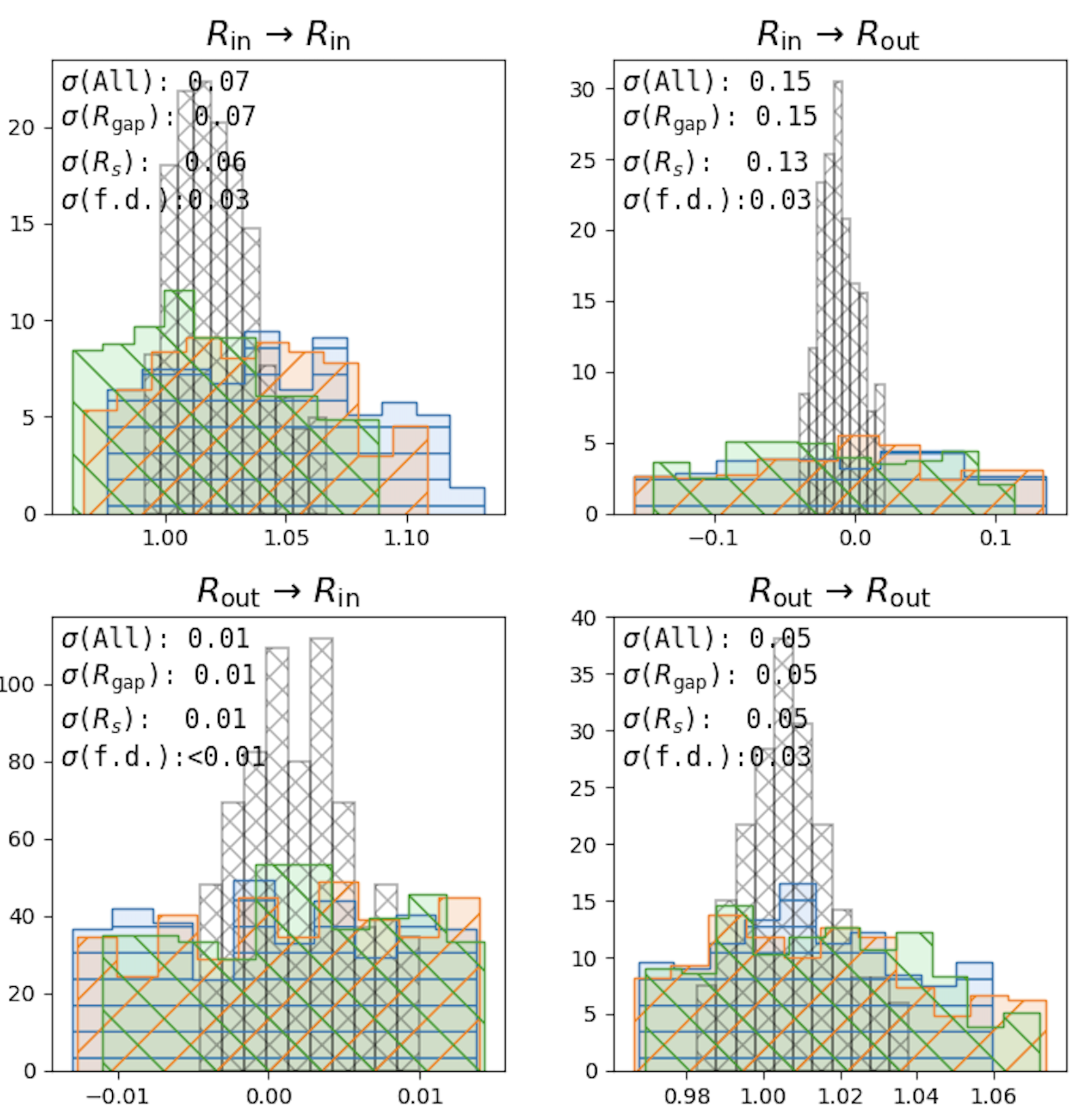
Machine learning has recently been adopted to emulate sensitivity matrices for real-time magnetic control of tokamak plasmas. However, these approaches would benefit from a quantification of possible inaccuracies. We report on two aspects of real-time applicability of emulators. First, we quantify the agreement of target displacement from VCs computed via Jacobians of the shape emulators with those from finite differences Jacobians on exact Grad-Shafranov solutions. Good agreement (≈5-10%) can be achieved on a selection of geometric targets using combinations of neural network emulators with ≈1e5 parameters. A sample of ≈1e5−1e6 synthetic equilibria is essential to train emulators that are not over-regularised or overfitting. Smaller models trained on the shape targets may be further fine-tuned to better fit the Jacobians. Second, we address the effect of vessel currents that are not directly measured in real-time and are typically subsumed into effective "shaping currents" when designing virtual circuits. We demonstrate that shaping currents can be inferred via simple linear regression on a trailing window of active coil current measurements with residuals of only a few Ampères, enabling a choice for the most appropriate shaping currents at any point in a shot. While these results are based on historic shot data and simulations tailored to MAST-U, they indicate that emulators with few-millisecond latency can be developed for robust real-time plasma shape control in existing and upcoming tokamaks.
Plasma shape control Virtual circuits Neural network emulation MHD equilibria MAST-U
Real-time applicability of emulated virtual circuits for tokamak plasma shape control
P. Cavestany, A. Ross, A. Agnello, A. Garrod, N. Amorisco, G. K. Holt, K. Pentland, J. Buchanan
2025 IEEE Conference on Control Technology and Applications
Machine learning has recently been adopted to emulate sensitivity matrices for real-time magnetic control of tokamak plasmas. However, these approaches would benefit from a quantification of possible inaccuracies. We report on two aspects of real-time applicability of emulators. First, we quantify the agreement of target displacement from VCs computed via Jacobians of the shape emulators with those from finite differences Jacobians on exact Grad-Shafranov solutions. Good agreement (≈5-10%) can be achieved on a selection of geometric targets using combinations of neural network emulators with ≈1e5 parameters. A sample of ≈1e5−1e6 synthetic equilibria is essential to train emulators that are not over-regularised or overfitting. Smaller models trained on the shape targets may be further fine-tuned to better fit the Jacobians. Second, we address the effect of vessel currents that are not directly measured in real-time and are typically subsumed into effective "shaping currents" when designing virtual circuits. We demonstrate that shaping currents can be inferred via simple linear regression on a trailing window of active coil current measurements with residuals of only a few Ampères, enabling a choice for the most appropriate shaping currents at any point in a shot. While these results are based on historic shot data and simulations tailored to MAST-U, they indicate that emulators with few-millisecond latency can be developed for robust real-time plasma shape control in existing and upcoming tokamaks.
Plasma shape control Virtual circuits Neural network emulation MHD equilibria MAST-U

Bayesian optimisation of poloidal field coil positions in tokamaks
T. Nunn, K. Pentland, V. Gopakumar, J. Buchanan
Physics of Plasmas
The tokamak is a world-leading concept for producing sustainable energy via magnetically-confined nuclear fusion. Identifying where to position the magnets within a tokamak, specifically the poloidal field (PF) coils, is a design problem which requires balancing a number of competing economic, physical, and engineering objectives and constraints. In this paper, we show that multi-objective Bayesian optimisation (BO), an iterative optimisation technique utilising probabilistic machine learning models, can effectively explore this complex design space and return several optimal PF coil sets. These solutions span the Pareto front, a subset of the objective space that optimally satisfies the specified objective functions. We outline an easy-to-use BO framework and demonstrate that it outperforms alternative optimisation techniques while using significantly fewer computational resources. Our results show that BO is a promising technique for fusion design problems that rely on computationally demanding high-fidelity simulations.
Bayesian optimisation Poloidal field coils Spherical tokamak MHD equilibria FreeGS
Bayesian optimisation of poloidal field coil positions in tokamaks
T. Nunn, K. Pentland, V. Gopakumar, J. Buchanan
Physics of Plasmas
The tokamak is a world-leading concept for producing sustainable energy via magnetically-confined nuclear fusion. Identifying where to position the magnets within a tokamak, specifically the poloidal field (PF) coils, is a design problem which requires balancing a number of competing economic, physical, and engineering objectives and constraints. In this paper, we show that multi-objective Bayesian optimisation (BO), an iterative optimisation technique utilising probabilistic machine learning models, can effectively explore this complex design space and return several optimal PF coil sets. These solutions span the Pareto front, a subset of the objective space that optimally satisfies the specified objective functions. We outline an easy-to-use BO framework and demonstrate that it outperforms alternative optimisation techniques while using significantly fewer computational resources. Our results show that BO is a promising technique for fusion design problems that rely on computationally demanding high-fidelity simulations.
Bayesian optimisation Poloidal field coils Spherical tokamak MHD equilibria FreeGS
Multiple solutions to the static forward free-boundary Grad-Shafranov problem on MAST-U
K. Pentland, N. C. Amorisco, P. E. Farrell, C. J. Ham
Nuclear Fusion
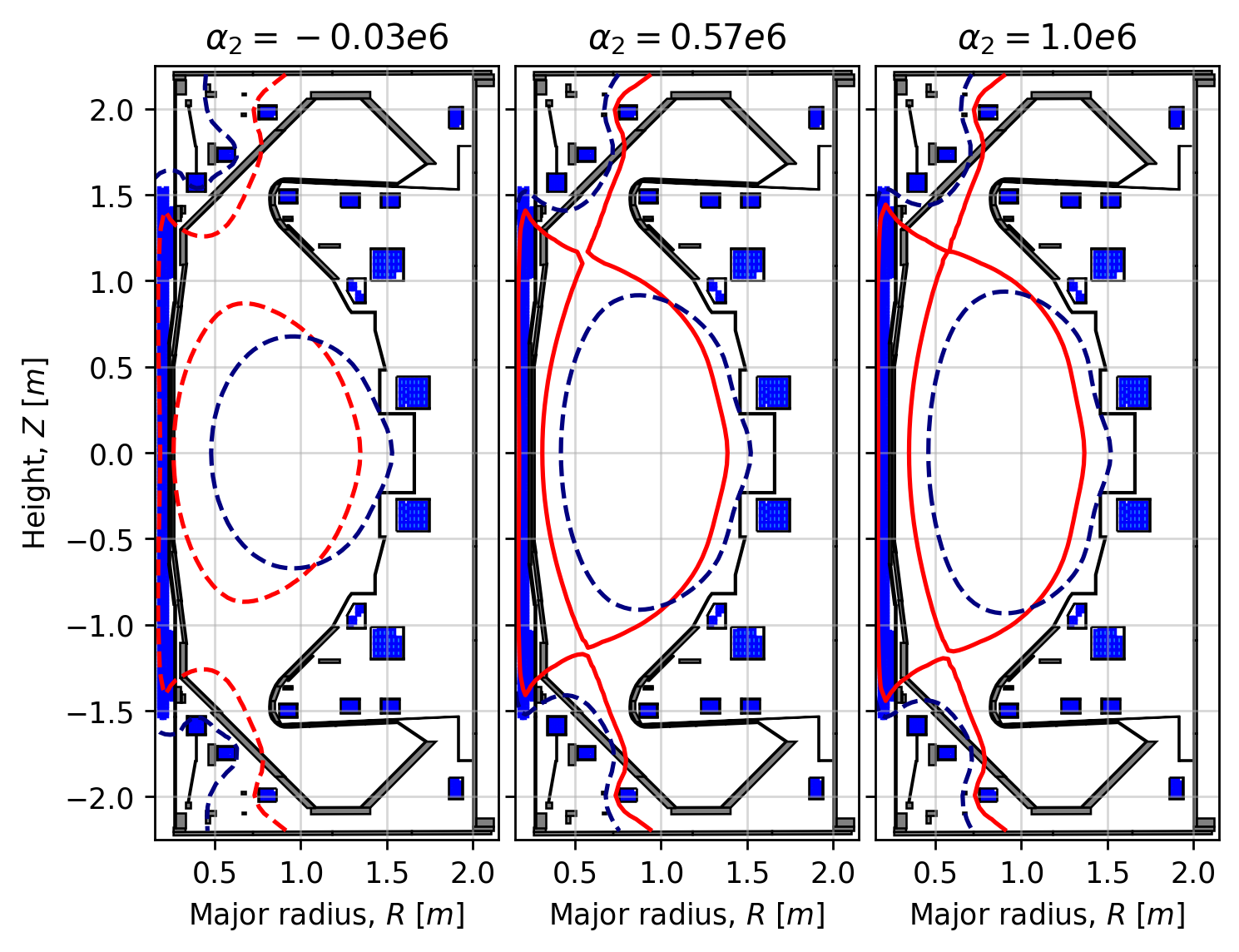
The Grad-Shafranov (GS) equation is a nonlinear elliptic partial differential equation that governs the ideal magnetohydrodynamic equilibrium of a tokamak plasma. Previous studies have demonstrated the existence of multiple solutions to the GS equation when solved in idealistic geometries with simplified plasma current density profiles and boundary conditions. Until now, the question of whether multiple equilibria might exist in real-world tokamak geometries with more complex current density profiles and integral free-boundary conditions (commonly used in production-level equilibrium codes) has remained unanswered. In this work, we discover multiple solutions to the static forward free-boundary GS problem in the MAST-U tokamak geometry using the validated evolutive equilibrium solver FreeGSNKE and the deflated continuation algorithm. By varying the plasma current, current density profile coefficients, or coil currents in the GS equation, we identify and characterise distinct equilibrium solutions, including both deeply and more shallowly confined plasma states. We suggest that the existence of even more equilibria is likely prohibited by the restrictive nature of the integral free-boundary condition, which globally couples poloidal fluxes on the computational boundary with those on the interior. We conclude by discussing the implications of these findings for wider equilibrium modelling and emphasise the need to explore whether multiple solutions are present in other equilibrium codes and tokamaks, as well as their potential impact on downstream simulations that rely on GS equilibria.
Multiple solutions Grad-Shafranov MHD equilibria FreeGSNKE Deflated continuation MAST-U
Multiple solutions to the static forward free-boundary Grad-Shafranov problem on MAST-U
K. Pentland, N. C. Amorisco, P. E. Farrell, C. J. Ham
Nuclear Fusion
The Grad-Shafranov (GS) equation is a nonlinear elliptic partial differential equation that governs the ideal magnetohydrodynamic equilibrium of a tokamak plasma. Previous studies have demonstrated the existence of multiple solutions to the GS equation when solved in idealistic geometries with simplified plasma current density profiles and boundary conditions. Until now, the question of whether multiple equilibria might exist in real-world tokamak geometries with more complex current density profiles and integral free-boundary conditions (commonly used in production-level equilibrium codes) has remained unanswered. In this work, we discover multiple solutions to the static forward free-boundary GS problem in the MAST-U tokamak geometry using the validated evolutive equilibrium solver FreeGSNKE and the deflated continuation algorithm. By varying the plasma current, current density profile coefficients, or coil currents in the GS equation, we identify and characterise distinct equilibrium solutions, including both deeply and more shallowly confined plasma states. We suggest that the existence of even more equilibria is likely prohibited by the restrictive nature of the integral free-boundary condition, which globally couples poloidal fluxes on the computational boundary with those on the interior. We conclude by discussing the implications of these findings for wider equilibrium modelling and emphasise the need to explore whether multiple solutions are present in other equilibrium codes and tokamaks, as well as their potential impact on downstream simulations that rely on GS equilibria.
Multiple solutions Grad-Shafranov MHD equilibria FreeGSNKE Deflated continuation MAST-U
2024
Validation of the static forward Grad-Shafranov equilibrium solvers in FreeGSNKE and Fiesta using EFIT++ reconstructions from MAST-U
K. Pentland, N. C. Amorisco, O. El-Zobaidi, S. Etches, A. Agnello, G. K. Holt, A. Ross, C. Vincent, J. Buchanan, S. J. P. Pamela, G. McArdle, L. Kogan, G. Cunningham
Physica Scripta
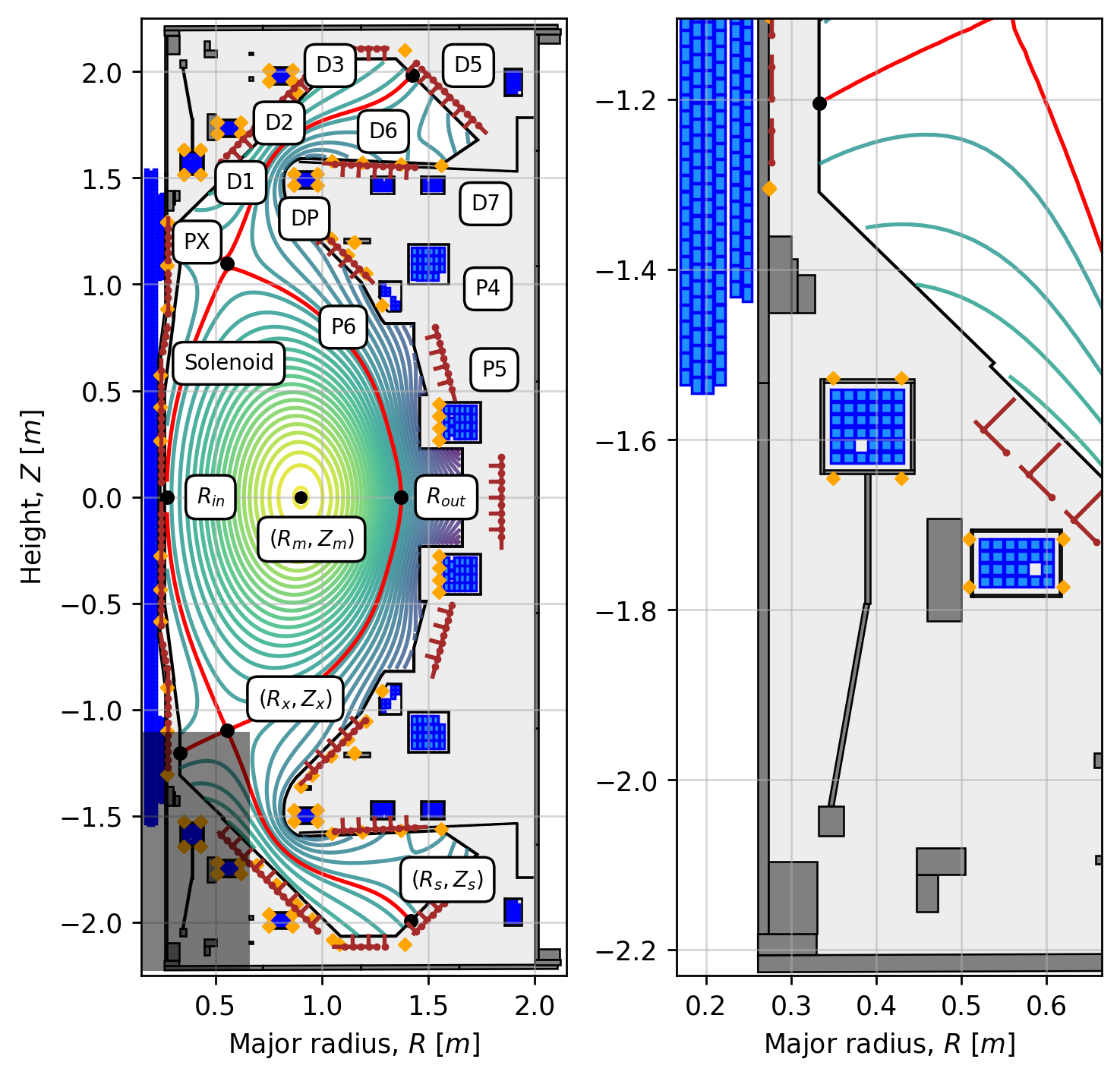
In this paper, we are interested in solving the static forward Grad-Shafranov (GS) problem for free-boundary MHD equilibria. Our focus is on the validation of the static forward solver in the Python-based equilibrium code FreeGSNKE by solving equilibria from magnetics-only EFIT++ reconstructions of MAST-U shots. In addition, we also validate FreeGSNKE against equilibria simulated using the well-established MATLAB-based equilibrium code Fiesta. To do this, we develop a computational pipeline that allows one to load the same (a)symmetric MAST-U machine description into each solver, specify the required inputs (active/passive conductor currents, plasma profiles and coefficients, etc.) from EFIT++, and solve the GS equation for all available time slices across a shot. For a number of different MAST-U shots, we demonstrate that both FreeGSNKE and Fiesta can successfully reproduce various poloidal flux quantities and shape targets (e.g. midplane radii, magnetic axes, separatrices, X-points, and strikepoints) in agreement with EFIT++ calculations to a very high degree of accuracy.
[Publication] [arXiv] [Code] [Poster] [Talk]
MHD equilibria Grad-Shafranov FreeGSNKE Fiesta EFIT++ MAST-U
Validation of the static forward Grad-Shafranov equilibrium solvers in FreeGSNKE and Fiesta using EFIT++ reconstructions from MAST-U
K. Pentland, N. C. Amorisco, O. El-Zobaidi, S. Etches, A. Agnello, G. K. Holt, A. Ross, C. Vincent, J. Buchanan, S. J. P. Pamela, G. McArdle, L. Kogan, G. Cunningham
Physica Scripta
In this paper, we are interested in solving the static forward Grad-Shafranov (GS) problem for free-boundary MHD equilibria. Our focus is on the validation of the static forward solver in the Python-based equilibrium code FreeGSNKE by solving equilibria from magnetics-only EFIT++ reconstructions of MAST-U shots. In addition, we also validate FreeGSNKE against equilibria simulated using the well-established MATLAB-based equilibrium code Fiesta. To do this, we develop a computational pipeline that allows one to load the same (a)symmetric MAST-U machine description into each solver, specify the required inputs (active/passive conductor currents, plasma profiles and coefficients, etc.) from EFIT++, and solve the GS equation for all available time slices across a shot. For a number of different MAST-U shots, we demonstrate that both FreeGSNKE and Fiesta can successfully reproduce various poloidal flux quantities and shape targets (e.g. midplane radii, magnetic axes, separatrices, X-points, and strikepoints) in agreement with EFIT++ calculations to a very high degree of accuracy.
[Publication] [arXiv] [Code] [Poster] [Talk]
MHD equilibria Grad-Shafranov FreeGSNKE Fiesta EFIT++ MAST-U
Neural-Parareal: dynamically training neural operators as coarse solvers for time-parallelisation of fusion MHD simulations
S. J. P. Pamela, N. Carey, J. Brandstetter, R. Akers, L. Zanisi, J. Buchanan, V. Gopakumar, M. Hoelzl, G. Huijsmans, K. Pentland, T. James, G. Antonucci, The JOREK Team
Computer Physics Communications
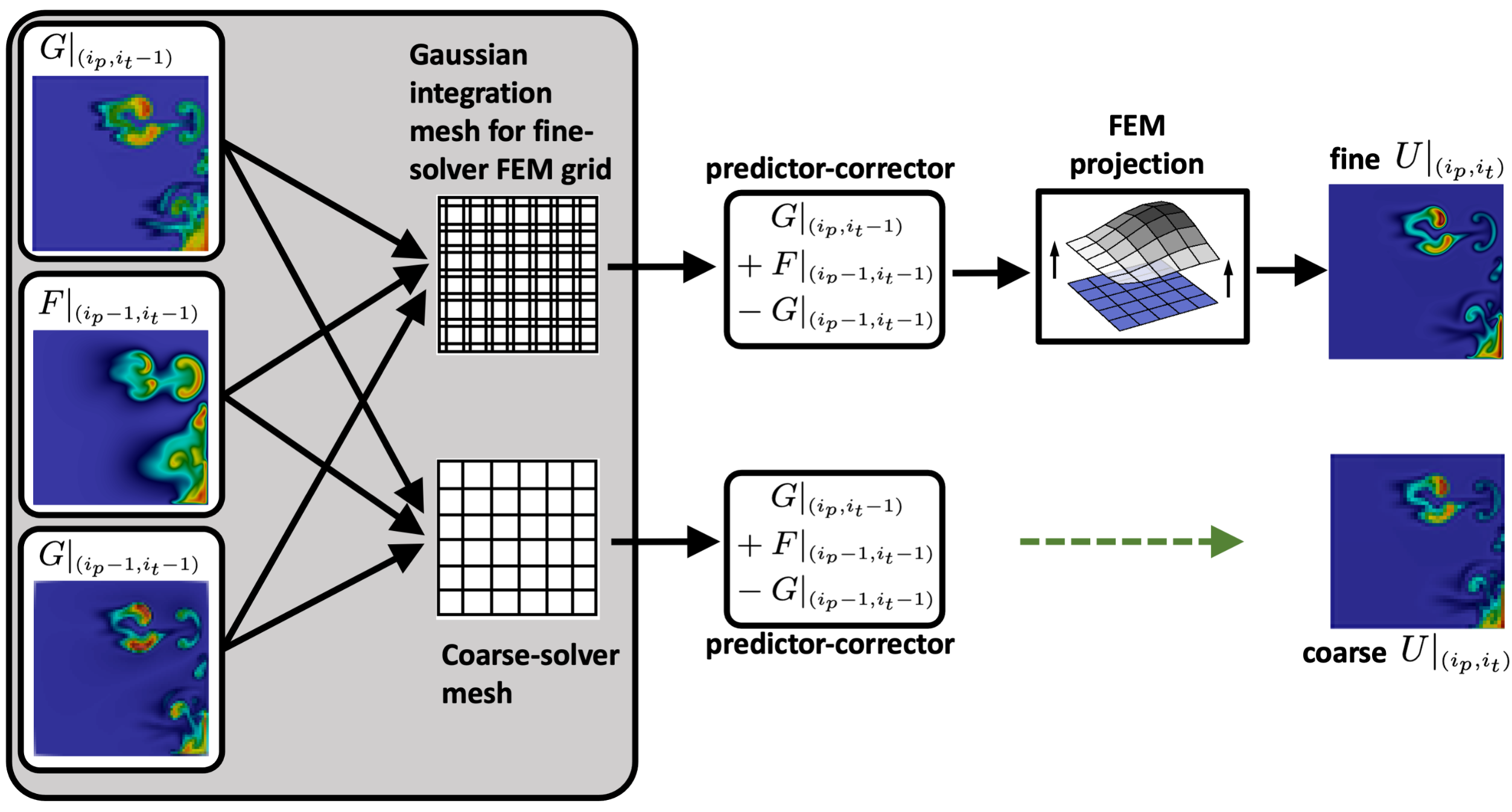
In this paper, we developed the Neural-Parareal framework to enhance the efficiency of time-parallel simulations for fusion research by integrating neural operators that dynamically train as new data becomes available. This approach replaces traditional coarse-solvers with neural network surrogates, leading to progressively more accurate predictions and significant speed-ups in the parareal simulations. Our findings demonstrate the effective convergence of high-performance computing and artificial intelligence, advocating for their common use in digital engineering design.
Fourier neural operators Parallel-in-time Parareal High performance computing
Neural-Parareal: dynamically training neural operators as coarse solvers for time-parallelisation of fusion MHD simulations
S. J. P. Pamela, N. Carey, J. Brandstetter, R. Akers, L. Zanisi, J. Buchanan, V. Gopakumar, M. Hoelzl, G. Huijsmans, K. Pentland, T. James, G. Antonucci, The JOREK Team
Computer Physics Communications
In this paper, we developed the Neural-Parareal framework to enhance the efficiency of time-parallel simulations for fusion research by integrating neural operators that dynamically train as new data becomes available. This approach replaces traditional coarse-solvers with neural network surrogates, leading to progressively more accurate predictions and significant speed-ups in the parareal simulations. Our findings demonstrate the effective convergence of high-performance computing and artificial intelligence, advocating for their common use in digital engineering design.
Fourier neural operators Parallel-in-time Parareal High performance computing
2023
Towards probabilistic time-parallel algorithms for solving initial value problems
K. Pentland
PhD Thesis
In this thesis, we focus on developing probabilistic time-parallel algorithms to efficiently solve computationally intensive initial value problems (IVPs). We introduce SParareal, a sampling-based algorithm that accelerates convergence by drawing candidate solution values from probability distributions derived from fine and coarse solution data, and GParareal, a learning-based algorithm that employs a Gaussian process emulator to enhance the predictor-corrector scheme. Both algorithms demonstrate improved numerical speedup and accuracy while providing stochastic solutions that quantify uncertainty, with GParareal uniquely leveraging legacy solution data from previous simulations.
Parallel-in-time Parareal Stochastic methods Gaussian processes Error bound analysis High performance computing
Towards probabilistic time-parallel algorithms for solving initial value problems
K. Pentland
PhD Thesis
In this thesis, we focus on developing probabilistic time-parallel algorithms to efficiently solve computationally intensive initial value problems (IVPs). We introduce SParareal, a sampling-based algorithm that accelerates convergence by drawing candidate solution values from probability distributions derived from fine and coarse solution data, and GParareal, a learning-based algorithm that employs a Gaussian process emulator to enhance the predictor-corrector scheme. Both algorithms demonstrate improved numerical speedup and accuracy while providing stochastic solutions that quantify uncertainty, with GParareal uniquely leveraging legacy solution data from previous simulations.
Parallel-in-time Parareal Stochastic methods Gaussian processes Error bound analysis High performance computing
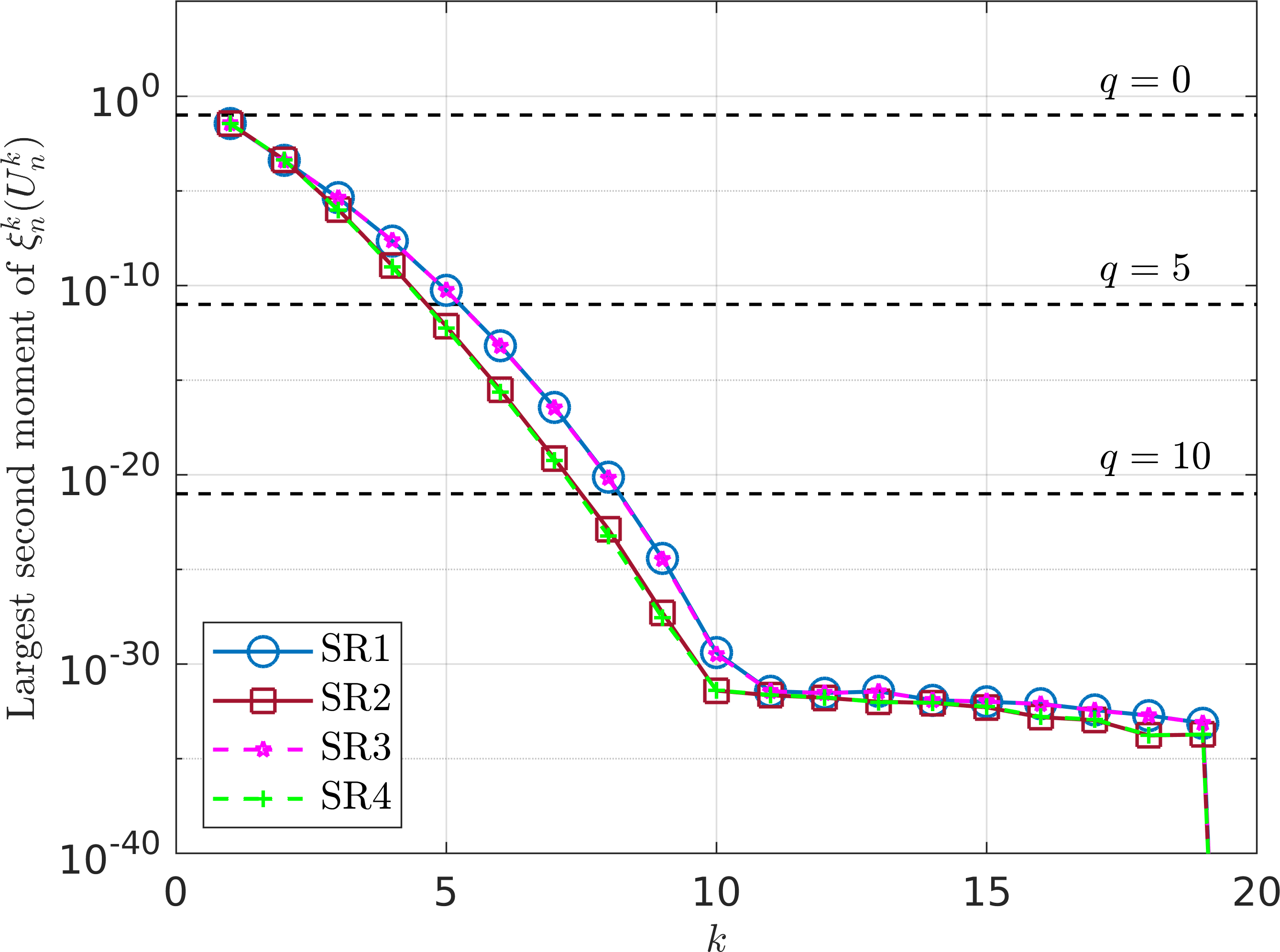
Error bound analysis of the stochastic parareal algorithm
K. Pentland, M. Tamborrino, T. J. Sullivan
SIAM Journal on Scientific Computing
In this paper, we derived both linear and superlinear mean-square error bounds for the stochastic parareal algorithm, a probabilistic variant of the parareal algorithm. We validated these theoretical results through numerical examples involving both linear and nonlinear ordinary differential equations.
Parallel-in-time Parareal Error bound analysis
Error bound analysis of the stochastic parareal algorithm
K. Pentland, M. Tamborrino, T. J. Sullivan
SIAM Journal on Scientific Computing
In this paper, we derived both linear and superlinear mean-square error bounds for the stochastic parareal algorithm, a probabilistic variant of the parareal algorithm. We validated these theoretical results through numerical examples involving both linear and nonlinear ordinary differential equations.
Parallel-in-time Parareal Error bound analysis
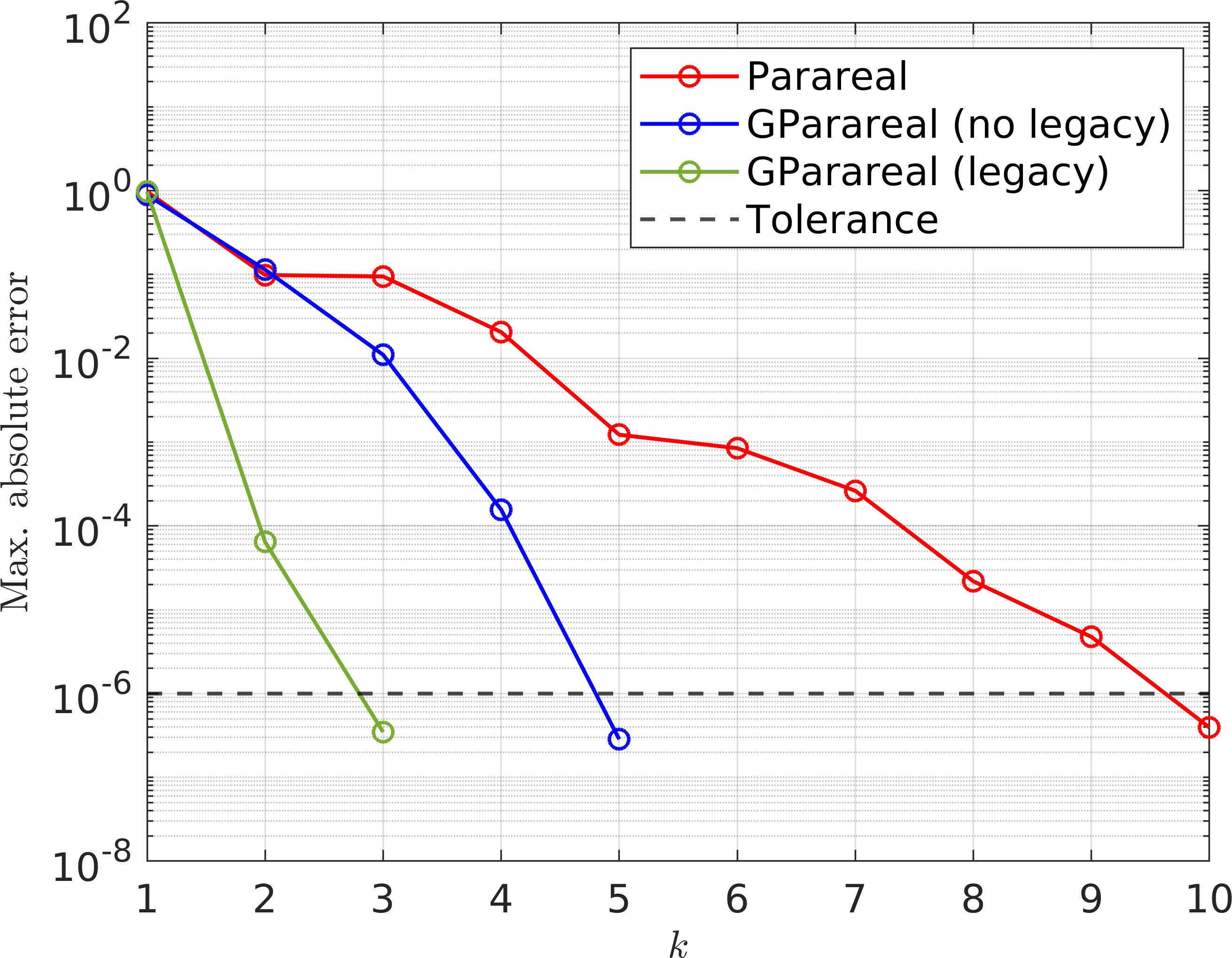
GParareal: a time-parallel ODE solver using Gaussian process emulation
K. Pentland, M. Tamborrino, T. J. Sullivan, J. Buchanan, L. C. Appel
Statistics and Computing
In this paper, we introduced GParareal, a time-parallel algorithm for solving initial value problems (IVPs) by employing a Gaussian process emulator to model the correction term between coarse and fine solutions. Our results demonstrate that GParareal converges in fewer iterations than the traditional parareal method, improving computational speed and enabling the use of legacy solution archives to further enhance convergence. This approach addresses limitations in existing time-parallel methods and offers a significant advancement in solving IVPs with high numerical accuracy.
[Publication] [arXiv] [Code] [Poster] [Talk]
Parallel-in-time Parareal Gaussian processes
GParareal: a time-parallel ODE solver using Gaussian process emulation
K. Pentland, M. Tamborrino, T. J. Sullivan, J. Buchanan, L. C. Appel
Statistics and Computing
In this paper, we introduced GParareal, a time-parallel algorithm for solving initial value problems (IVPs) by employing a Gaussian process emulator to model the correction term between coarse and fine solutions. Our results demonstrate that GParareal converges in fewer iterations than the traditional parareal method, improving computational speed and enabling the use of legacy solution archives to further enhance convergence. This approach addresses limitations in existing time-parallel methods and offers a significant advancement in solving IVPs with high numerical accuracy.
[Publication] [arXiv] [Code] [Poster] [Talk]
Parallel-in-time Parareal Gaussian processes
2022
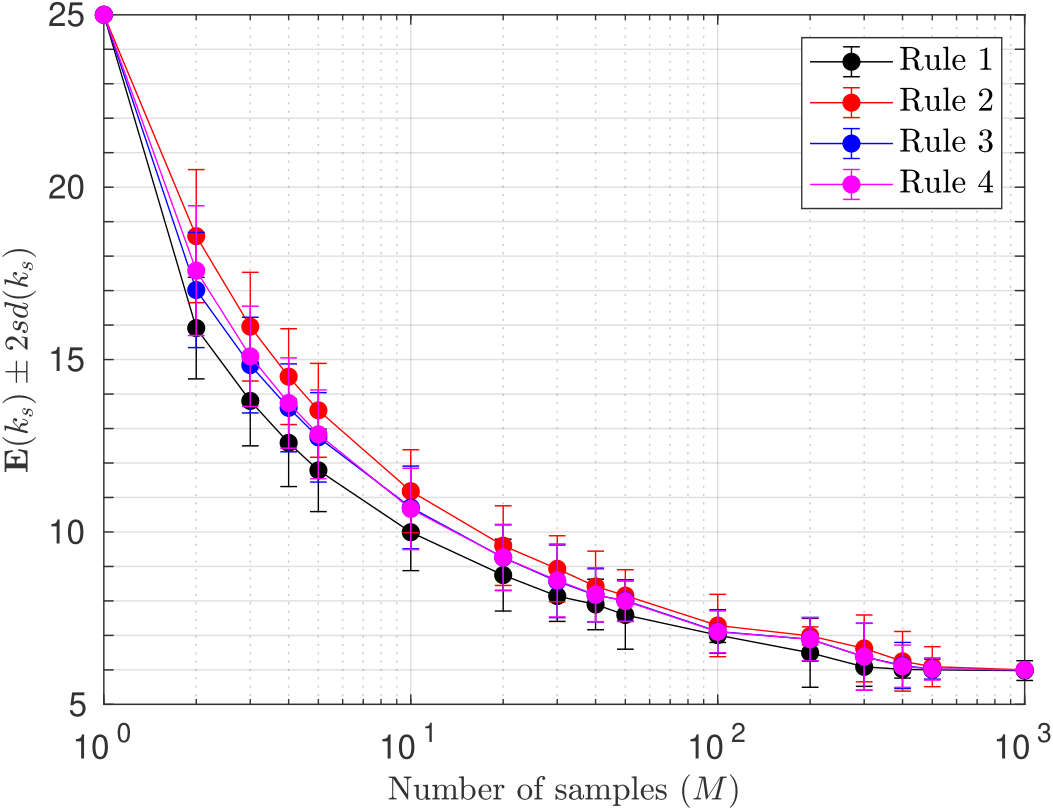
Stochastic parareal: an application of probabilistic methods to time-parallelisation
K. Pentland, M. Tamborrino, D. Samaddar, L. C. Appel
SIAM Journal on Scientific Computing
In this paper, we introduced a stochastic variant of the parareal algorithm to speed up its convergence when solving time-dependent differential equations. By sampling initial values from dynamically varying probability distributions and selecting the smoothest trajectories in time, the algorithm converges in fewer iterations compared to the traditional deterministic approach. Our results show that stochastic parareal reduces iteration counts while maintaining accuracy, with potential to capture uncertainty in the solution.
[Publication] [arXiv] [Code] [Poster] [Talk]
Parallel-in-time Parareal Probabilistic numerics
Stochastic parareal: an application of probabilistic methods to time-parallelisation
K. Pentland, M. Tamborrino, D. Samaddar, L. C. Appel
SIAM Journal on Scientific Computing
In this paper, we introduced a stochastic variant of the parareal algorithm to speed up its convergence when solving time-dependent differential equations. By sampling initial values from dynamically varying probability distributions and selecting the smoothest trajectories in time, the algorithm converges in fewer iterations compared to the traditional deterministic approach. Our results show that stochastic parareal reduces iteration counts while maintaining accuracy, with potential to capture uncertainty in the solution.
[Publication] [arXiv] [Code] [Poster] [Talk]
Parallel-in-time Parareal Probabilistic numerics
2020
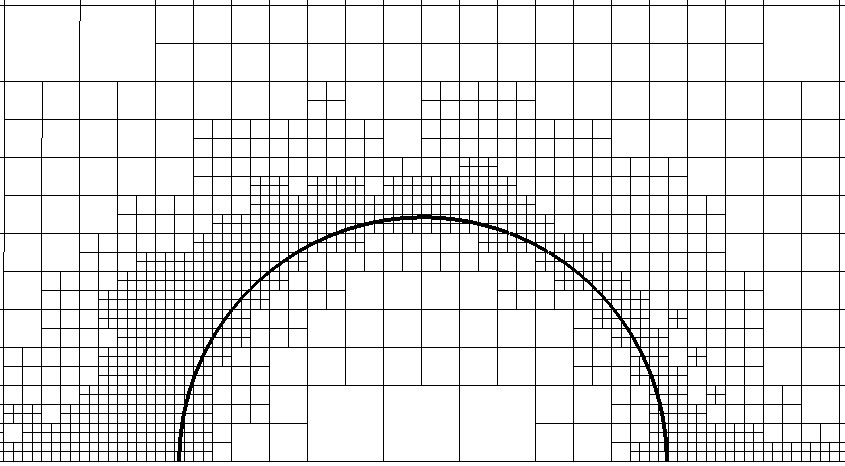
Hats and pancakes in the sky: high-speed droplet dynamics
K. Pentland, R. Cimpeanu, E. Brambley
MSc Project
In this project, we explored improvements to an existing model that predicts the trajectory and deformation of water droplets impacting aircraft surfaces, focusing on the critical effects of high-speed airflows. Using sensitivity analysis and high-resolution direct numerical simulations (DNS), we identified key influencing parameters and improved the accuracy of the model. Our results highlight the potential of DNS for more precise simulation of droplet behavior in complex flow conditions.
Direct numerical simulations Multiscale modelling Two-phase fluids
Hats and pancakes in the sky: high-speed droplet dynamics
K. Pentland, R. Cimpeanu, E. Brambley
MSc Project
In this project, we explored improvements to an existing model that predicts the trajectory and deformation of water droplets impacting aircraft surfaces, focusing on the critical effects of high-speed airflows. Using sensitivity analysis and high-resolution direct numerical simulations (DNS), we identified key influencing parameters and improved the accuracy of the model. Our results highlight the potential of DNS for more precise simulation of droplet behavior in complex flow conditions.
Direct numerical simulations Multiscale modelling Two-phase fluids
2019
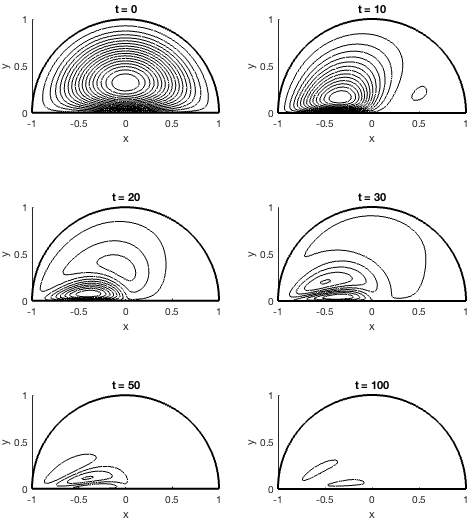
Spin-down in the absence of reflected waves
K. Pentland, E. Johnson
MSc Project
The aim of this project was to reproduce the 3D FEM HPC simulation results of Li et al. (2012) that claimed "no discrete set of oscillatory modes exist in a spin-down fluid within a half-cone geometry" using much simpler techniques. To do this, we derived a 2D topographic wave equation for the half-cone geometry and used both spectral methods and eigenmode analysis to recreate the numerical results. In fact, we disprove their conclusion that no oscillatory modes exist because of the half-cone's vertex, demonstrating instead that no modes exist only when the depth of the half-cone container goes to zero.
Topographic wave equation Spectral methods Eigenmode analysis
Spin-down in the absence of reflected waves
K. Pentland, E. Johnson
MSc Project
The aim of this project was to reproduce the 3D FEM HPC simulation results of Li et al. (2012) that claimed "no discrete set of oscillatory modes exist in a spin-down fluid within a half-cone geometry" using much simpler techniques. To do this, we derived a 2D topographic wave equation for the half-cone geometry and used both spectral methods and eigenmode analysis to recreate the numerical results. In fact, we disprove their conclusion that no oscillatory modes exist because of the half-cone's vertex, demonstrating instead that no modes exist only when the depth of the half-cone container goes to zero.
Topographic wave equation Spectral methods Eigenmode analysis
2017
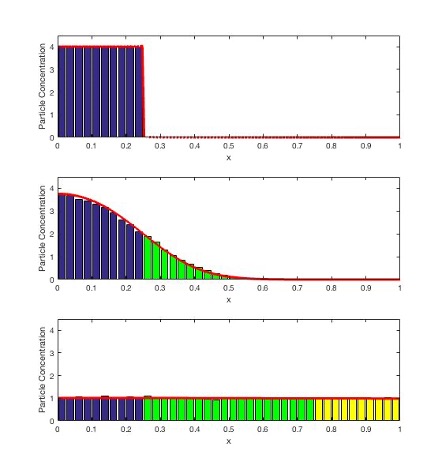
A blending hybrid model for simulating reaction-diffusion equations
K. Pentland, C. A. Yates
Undergraduate Summer Research Project
The main focus of this project was to speed up the simulation time of reaction-diffusion systems. We did this by developing an algorithm that tracks the concentration of the quantity of interest using "compartments" in one region of the spatial domain, using individual "molecules" in another region, and then a "blend" of both in the overlapping region. This resulted in a hybrid "blending" method for simulating reaction-diffsuion systems.
Reaction-Diffusion PDEs Gillespie algorithm Brownian motion
A blending hybrid model for simulating reaction-diffusion equations
K. Pentland, C. A. Yates
Undergraduate Summer Research Project
The main focus of this project was to speed up the simulation time of reaction-diffusion systems. We did this by developing an algorithm that tracks the concentration of the quantity of interest using "compartments" in one region of the spatial domain, using individual "molecules" in another region, and then a "blend" of both in the overlapping region. This resulted in a hybrid "blending" method for simulating reaction-diffsuion systems.
Reaction-Diffusion PDEs Gillespie algorithm Brownian motion